
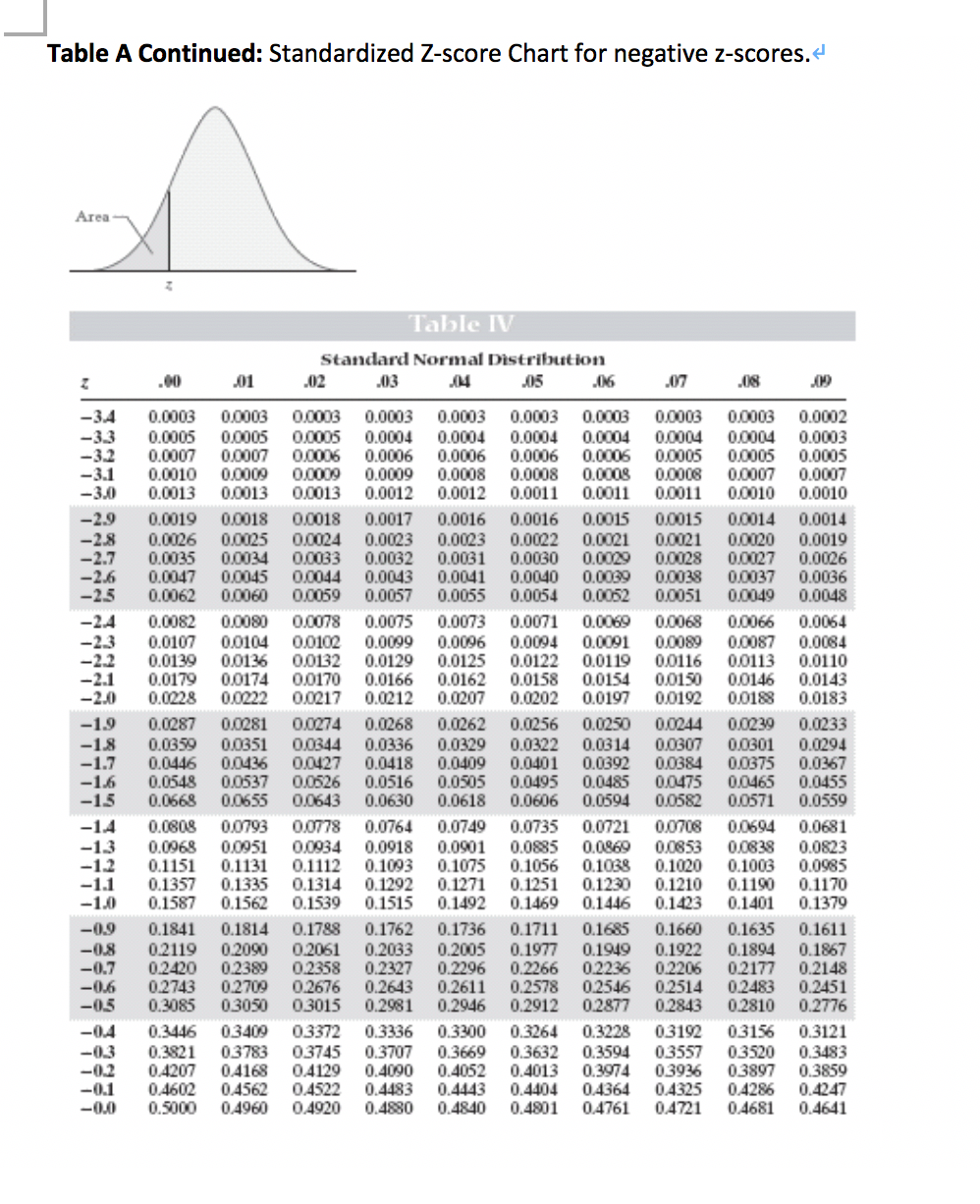
So there's a two centimeter one, there's another two centimeter one. So you discover, and these are all adults. Those lengths distributed? Lengths of winged turtles. Length and you also wanna care about, how are And so you go and you're actually able to measure all the winged turtles and you care about their

Seven winged turtles, the entire population of Species of winged turtles and there's a total of Type of marine biologist and you've discovered a new Now let's make that a little bit concrete. Number of standard deviationsįrom our population mean for a particular, particular data point. Of standard deviations away from the mean thatĪ certain data point is. And one way to think about a Z-score is it's just the number Most commonly used tools in all of statistics is Here's another, with the positive and negative signs on the opposite side:

Let's do the same thing with different values, one positive and one negative: We get the correct difference and the correct positive sign. If we subtract the mean from the point however: If we were taking the absolute value of the difference, this wouldn't matter, but here we want the difference and the direction. This would be the correct absolute difference of (3.7), but the negative symbol also implies that our data point, (-2.2), was below our mean, (-5.9), which of course is not true. Say we try to find the difference between the two by doing mean minus point: You'd still get the correct absolute value for each difference as long as you use the absolute value bars.īut here are some other examples with various negative and positive signs to prove that subtracting the data point minus the mean always works, but that the reverse (mean minus data point) doesn't work, with decimal places just to prove that's not a factor either in case you were curious, as I was): I will say that- unless there's a reason that becomes apparent later- it would probably be better practice to subtract the data point minus the mean when finding standard deviation too, just to be consistent.
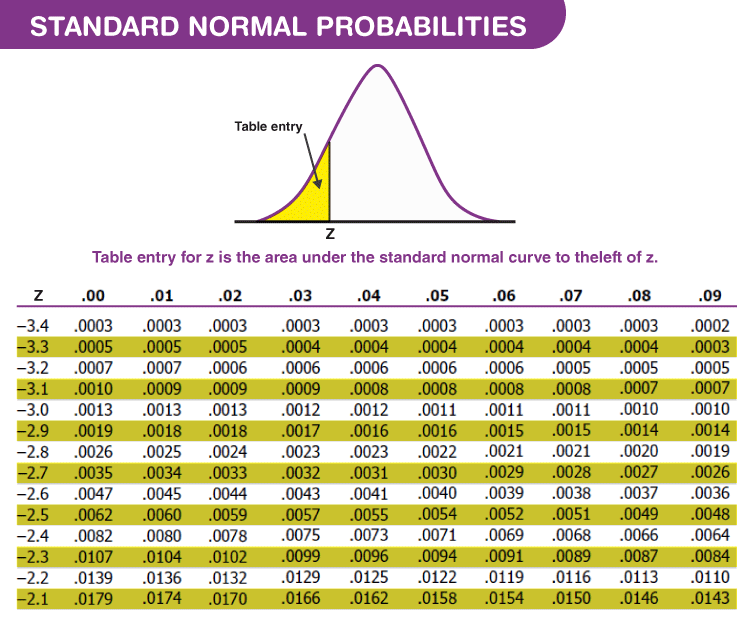
If we were to subtract the data point from the mean, (which would be (2) from (3), or (3) - (2)), we would get the same absolute difference between the two values but we might come away thinking our z-score is positive, since we'd get a positive difference of (1) before dividing by the standard deviation, which is always positive. When we subtract (3) from (2) to find the difference, that gives us a negative answer, (-1), which we then divide by the standard deviation to see how far the difference between the mean and the data point are, in terms of standard deviations (the definition of a z-score). Here we have a mean of (3), and a data point with a value of (2). If we didn't look at the absolute values, any dataset with both positive and negative data points would be messed up when we find the sum of each difference before dividing by (n) or (n-1) and then finding the square root. When finding the standard deviation this doesn't matter, since we're only interested in the absolute value of the discrepancy between each point and the mean, as standard deviation is an absolute value. We want the absolute difference between the numbers but also the direction the point is from the mean.


 0 kommentar(er)
0 kommentar(er)
